透過基因演算法尋找實數公式最佳解

前言

此研究配合論文內容進行實踐，一些公式的部分在此不進行介紹。有興趣的話可以自行查看論文喔~

研究摘要

基因演算法，經常被用來尋找範圍內的最佳解，無論是在數學或是科學領域，基因演算法可以協助我們更加快速的找到所需目標範圍內的最大或最小值。基因演算法整體架構主要分為三大部分:複製、交叉和突變，每一個部分都有它重要的意義存在。本研究裡也加入了田口的優化算法，使在尋找最佳解的過程中可以更為快速和精準，也可以有效提升基因多樣性並減少陷入局域最佳解的情況。

Introduction

基因演算法可以比擬為生物族群進化的過程，從染色體之間的前期複製，到彼此之間的交叉和代表進化的突變。在適者生存的條件下，基因演算法也具有與其相同的特性，在世代交替的同時，不停的將優秀的基因延續到下一代，甚至是更進一步創造出更適合當時限制環境下的個體。本實驗中每個族群個體有代表其的八個主要實數基因，每個基因都有不同的範圍限制，使它們不會超出所規定的限制。加上六個限制條件，更進一步的規定了每個基因所進化的方向。基因演算法能夠縮短尋找最優秀個體的時間，如若再加上促進其進化的手段，像是田口表算法，懲罰值的加入，將大大的提升它的可用性。 不同於一般的是，本論文裡所求得的最佳解為最小值，因此對於輪盤的排序必須進行人為的調整，以促使輪盤上只佔小面積的部分能夠被優先選擇。 本研究的動機在於課程上的學習與實踐操作，訓練學生程式撰寫能力的同時，讓我們能更深入的認識基因演算法的原理，並在遇到瓶頸時，能發散思維尋找解決的辦法，或是主動尋找資料解決問題。 我們將在第一部分介紹基因演算法的名詞解釋，接著是研究中的程式架構與分析，最後是基因演算法的結果展示。

Background Knowledge

基因演算法主要有三個階段:複製、交叉、突變。

複製:染色體依據適應函數值大小，決定該染色體生存至下一代的機率，因此適應函數值高的染色體將有較高之機率被自我大量複製而成為下一代的新染色體，適應函數值低的染色體可能遭到淘汰的命運。 複製方法一般較常被使用的是輪盤式選擇，依每依染色體適應函數值的大小來決定在輪盤上之大小。適應函數值越大者，則輪盤上所佔的面積越大，反之，若適應函數值越小，則輪盤上所佔的面積越小。被輪盤選中的染色體將送至交叉池裡，等待進行交叉的程序。

交叉:在複製完成後，被複製至交叉池之染色體便進行交叉的程序。以隨機的方式選擇兩個不同的染色體進行配對，藉由交換彼此之基因位元而產生新的染色 體，以此反覆地進行，累積上一代的優秀染色體，就可以產生更優秀的染色體。 在本篇論文裡選用的交叉模式為算術交叉法。在選取的兩個實數編碼的染色體中，隨機選取一交叉點，將交叉點之基因進行內積，且交叉點後的基因互換，即為新的染色體。

突變:在最佳化的問題裡，若僅有交叉的過程，尚不足以獲得最佳解，還必須搭配突變的運算方法，才能有效找到最佳解。交叉後的染色體，依據預設的突變率，以亂數(0~1)來決定染色體中的基因是否突變。在本篇研究中使用的是二實數編碼之非均勻突變。 實數編碼的非均勻突變:突變的染色體基因，因為小於預設突變率的基因，突變方式為在該變數目前值的附近進行微調，且隨著代數與指數的增加，微調的幅度將越來越小。在本篇研究裡，預設突變率為0.3，若產生的亂數值小於0.3，則該基因進行突變，並以隨機產生0和1的方式決定突破的方向，是向右突變以增加數值或是向左突變以減少數值。否則，繼續檢查所有的判斷式。

田口表:田口設計使用正交表，後者估計因數對回應均值和變異的效應。 正交表意味著設計是平衡的，即各個因數水平被賦予相等的權重。 因此，可以獨立於所有其他因數來評估每個因數，這樣，一個因數的效應便不會影響另一個因數的估計。 由此可以在使用部分因數設計時減少與試驗相關聯的時間和成本。田口表如下:

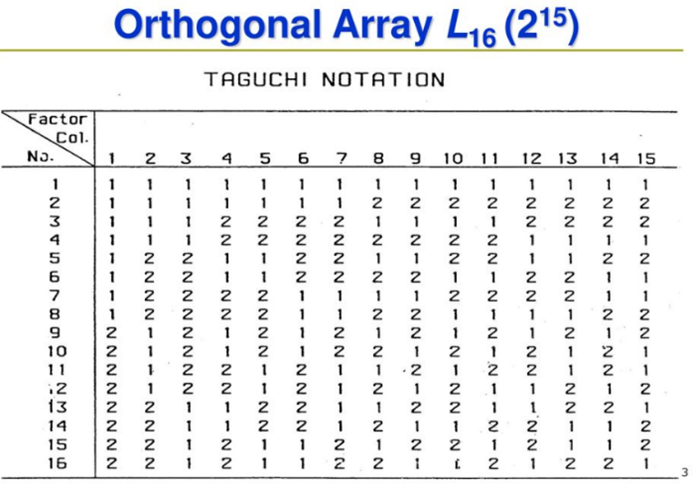田口計算方式

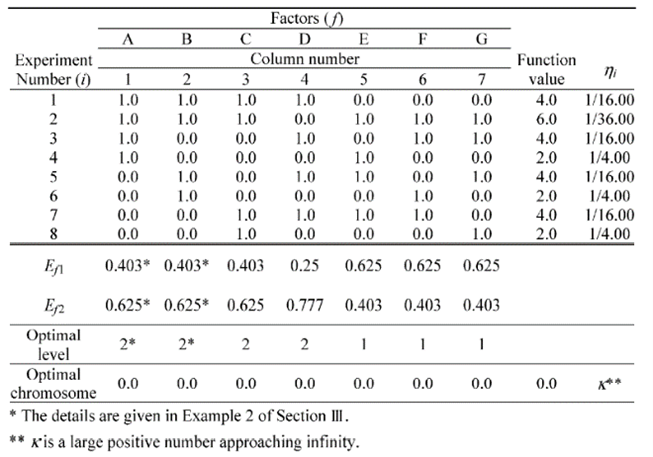Optimal level為該基因中Ef1和Ef2之間較高者的基因被選中，其中Ef1和Ef2的計算方式如下:

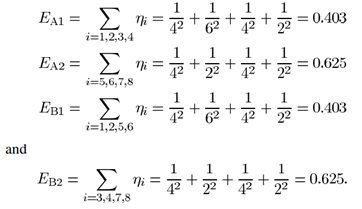田口的計算方式了解後，就可以帶入程式裡使用了，本研究設計的程式流程如下:

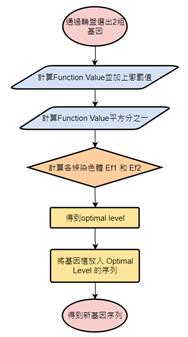在族群的生成方面，研究中採用("Jinn-Tsong Tsai,Improved differential evolution algorithm for nonlinear programming and engineering design problems,2014. ")的方式。在初始族群生成時，只規定每個基因的範圍值，不考量其餘6個判斷式帶入後的正確性。基因的生成採隨機的模式，並將每一組基因帶入6個判斷式測試是否合乎標準，若不符合，則在之後的適應函數值加入一極大值做為區隔，不再重新生成一組新的基因。因為我們所求為適應函數之極小值，故不符合標準之基因並不會一值保留在群體內部，在經過數代後它們會逐漸朝正確區塊靠近，直到8個基因符合。

在研究中程式採用C++語法，並以DEV-C++作為程式開發環境。首先以隨機方式生成200組的基因，並計算每組基因的適應函數值，同時將每個基因代入所規定的6個判斷式內檢測，若是不符合則在適應函數值處加入一極大值。

接著以模仿俄羅斯輪盤的方式製作一由適應函數值機率所構成的輪盤，並調整其機率使其較容以選中機率較小的區塊，因為在此研究中，我們所求為極小值，在輪盤上佔據較小面積的部分。

下一步轉動輪盤，一次選出兩組基因做算術交叉，然後再轉動一次輪盤做田口法優化。下一步基因突變，用不均勻突變的方式，以隨機亂數的方式決定族群裡的每個基因是否參與突變，選出來做突變的基因再以亂數的方式決定突變的方向，是變大或者變小。

基因突變結束後，算是完成一輪的基因演算法，但是，一輪並不足以找出所求的最佳解。因此我們將最後的基因重新代入判斷式檢查，在保留與母代相同族群數目的前提下，剔除由小到大排序後的末端基因，同時檢查族群裡基因的重複性，剃除裡面重複性過高的基因，並以隨機生成的方式遞補新的基因，以此確保族群裡的多樣性，減少陷入局域最佳解的處境。詳細流程圖如下:

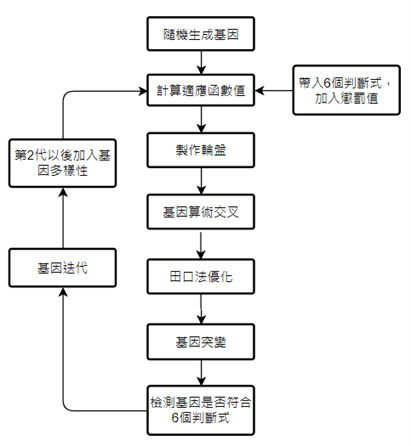
實驗與分析

我們對程式執行10次進行測試，詳細的記錄下每一輪測試所得到的結果，結果為以下表格:

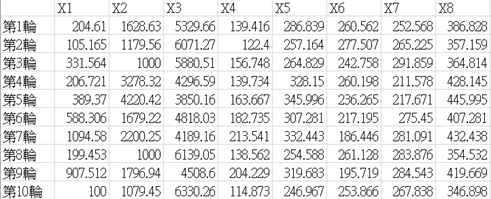執行10次每組基因

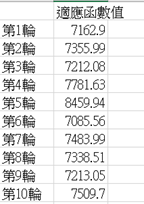執行10次每組適應函數值

從結果看出，每次執行的結過所得到的最小值不固定，從最小的7085.56到最大的8459.94。 所以單憑以上的執行結果我們並不能保證自己找到的就是極限的最小值，雖然大多數結過都是保持在七千以內，以此可以推定最小值應為7000到8000範圍內的某個數值。

參考文獻

[1] Jinn-Tsong Tsai,Improved differential evolution algorithm for nonlinear programming and engineering design problems,2014.
[2] Jinn-Tsong Tsai,Hybrid Taguchi-Genetic Algorithm for Global Numerical Optimization,2004.

C++ Genetic Algorithm 程式碼展示